最高のコレクション 双対グラフ 404041-双対グラフとは
双対グラフ(Dual Graph) •平面グラフMの各領域に1つの点を取り、隣接する 2つの領域の点を、その隣接する辺に交差する辺 で結ぶグラフM*は、Mの双対と呼ばれる。 11二部グラフ上の最大マッチング問題 入力:二部グラフG = (A;B;E) 目的:要素数が最大のマッチング 線形計画問題っぽく定式化してみる (整数計画問題) Minimize ∑ e2E x(e) subject to ∑ e2E v2e );; 「書き方」的に言うと、えとですね、元の平面グラフの辺に注目するんです。 で、元のグラフの各辺eについて、領域の組 {p, q}すべてについて、「その辺eだけを横切ってp, qを互いにつなぐように双対グラフの辺が描けるなら、それを1本だけ描く」んです。 (ただし {p, q}と {q, p}は同じものとみなして、区別しません。 ) 「領域の組 {p, q}すべて」とは言っても、「その辺eだけを横
逆構造定理の略証
双対グラフとは
双対グラフとは-The unique planar embedding of a cycle graph divides the plane into only two regions, the inside and outside of the cycle, by the Jordan curve theoremHowever, in an ncycle, these two regions are separated from each other by n different edges Therefore, the dual graph of the ncycle is a multigraph with two vertices (dual to the regions), connected to each other by n dual edges で、元のグラフの各辺eについて、領域の組 {p, q}すべてについて、「その辺eだけを横切ってp, qを互いにつなぐように双対グラフの辺が描けるなら、それを1本だけ描く」んです。 (ただし {p, q}と {q, p}は同じものとみなして、区別しません。 ) 「領域の組 {p, q}すべて」とは言っても、「その辺eだけを横切ってp, qを互いつなぐ」ことができるためには、pとqはどちらも「その辺e」
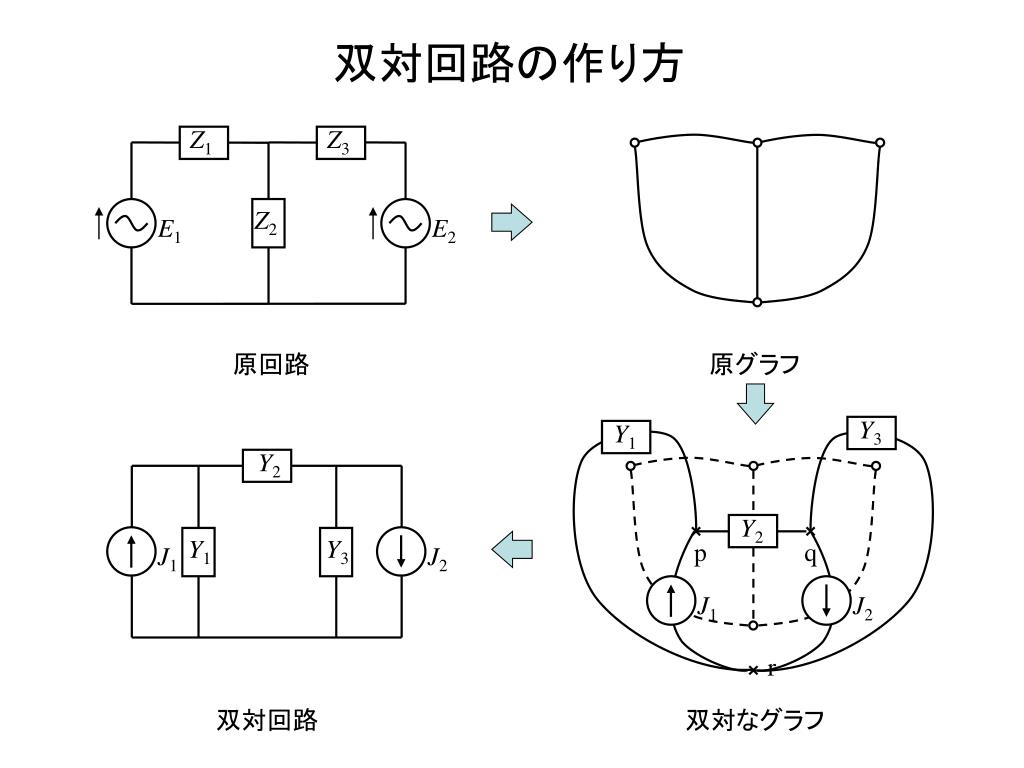



Ppt 電気回路学 Powerpoint Presentation Free Download Id
したがって,双対な回路同士では,表1の 左右が対応する。 12 双対回路を描く手順 平面上で線が交わらないように描ける回路の双対回路を次の手順で描くことが出来る。(平面 グラフ,K Kurtowski の定理=> 篠田:「回路論入門(1)」p238)) Step1 原回路の外側を囲むようにP0 線を描く。ウト手法は,盤面を双対グラフとして捉えたデータ 構造を利用し,勝利に必要なパスの探索を行うこと で高速化を図っている. 2 Hex 21 Hex のルール Hex は図1 のような六角形のセルが敷き詰められ た盤面で2 人で遊ぶゲームである.両プレイヤーは双対グラフの作り方から, 「グラフGの各面に双対グラフの点を打ち込む」ことからn∗ = f が, 「グラフ Gの各辺eに交差するように双対グラフの辺e∗ を描く」ということからm∗ = mが直ちに言える 一方, 双対グラフについてのオイラーの公式から f = n∗ =2m∗ −f∗ (318)
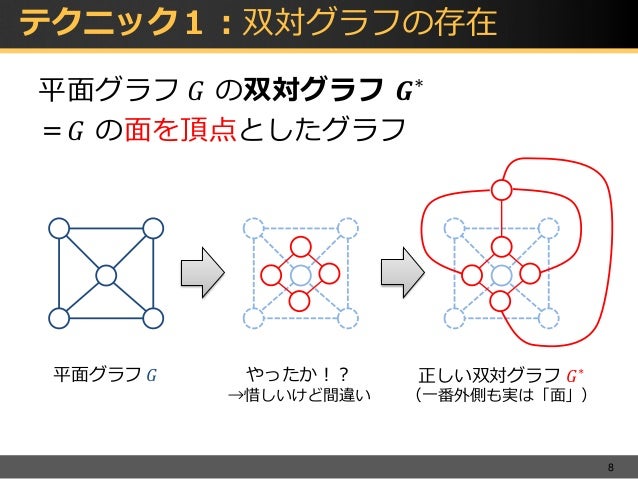
双対グラフ グラフ 𝐺𝐺 ∗から次の手続きにより得られるグラフ 𝐺𝐺 を 𝐺𝐺 の双対グラフという。 step ∗1 𝐺𝐺 の各領域 𝑟𝑟 𝑖𝑖 (無限領域も含む)に点 𝑃𝑃 𝑖𝑖∗ をとり、𝐺𝐺 の点とする。 step 2 𝐺𝐺 の各辺 𝑒𝑒 𝑖𝑖 に対し、𝑒𝑒 𝑖𝑖 を境界にもつ2つのの重要な特性としてのグラフ的,双対グラフ的という概 念とそれらの関連等について述べることにする 幾何的双対グラフと抽象的双対グラフ グラフGが与えられた時に,その双対グラブ (dual graph) として幾何的双対グラフと抽象的双対グラフのArial MS Pゴシック MS P明朝 Symbol Times New Roman 標準デザイン Microsoft 数式 30 電気回路学 連絡事項 講義日程と内容 線形回路 重ね合わせの理 重ね合わせの理の証明 重ね合わせの理の証明 重ね合わせの理 重ね合わせの理 重ね合わせの理 重ね合わせの理 出席レポート問題 双対性 双対回路 双対
一般のグラフで言える 2 つの重要な定理 二部グラフの最小点被覆、最大安定集合、最小辺被覆の具体的な構成について考えていきたいのですが、 最小点被覆だけ考えれば十分 です。 なぜなら二部グラフに限らず、一般のグラフで以下の 2 つのことが 双対定理の嬉しさ:最適性の証拠 双対問題を考えるメリットの一つとして 最適性の簡単な証拠を提示できる というのがあります。 強双対定理のおかげで,求めた答えが正しいことを簡単に他人に納得させることができます(どうやって答えを求めたかという複雑な手順を説明する必要が双対多面体 の用例・例文集 グラフの双対性は、双対多面体を位相幾何学的な視点から一般化したものである。歴史的に、双対グラフの概念は正多面体を双対多面体の組とみなすことができるという発見から始まった。角柱と双角錐は互いに双対多面体だが、円柱と双円錐の間にはそのような



より良い凸面分解を求めて Roblox Blog



早稲田教育叢書 31 数学教材としてのグラフ理論 鈴木 晋一 編著 早稲田大学 教育総合研究所
1決定リスト 2 分 2 分決定リスト 2 分決定図 2 分決定木 2 部 2 重 2 重Horn関数 2 重ホーン関数 2 重ホーン関数⇒ 2 重 Horn 関数2 部グラフ 2 重ホーン関数double Horn function⇒ 2 重 Horn 関数2 部グラフ 2 重否定律 2 項反転公式 2 項定理 2 項関係 Banzhaf指数 Bell数 Birkhoffの定理 Birkhoffの表現定理 Birkhoffバー 円の極と極線は、双対(そうつい)的な関係にあります。 双対性とは幾何学の重要な概念です。 この双対性について、極と極線を通して探っていきましょう。 円の極と極線が、そのまま三角形の極と極線に結びつき、様々な現象を示します。 極線上の点の極線が不思議な現象を示します。Gの双対は、同じ基本的な3正規グラフを持つGEMによって表されますが、エッジの色の2つが交換されています。 また、GEMによって表されるグラフは、そのすべての頂点サイクルを縮小し、平行エッジのペアを1つのエッジにマージすることによって形成できます。 したがって、Gの双対を作成すること(どの双対を気にしない限り)は、線形時間で簡単に実行できます。 — デビッド・エップス
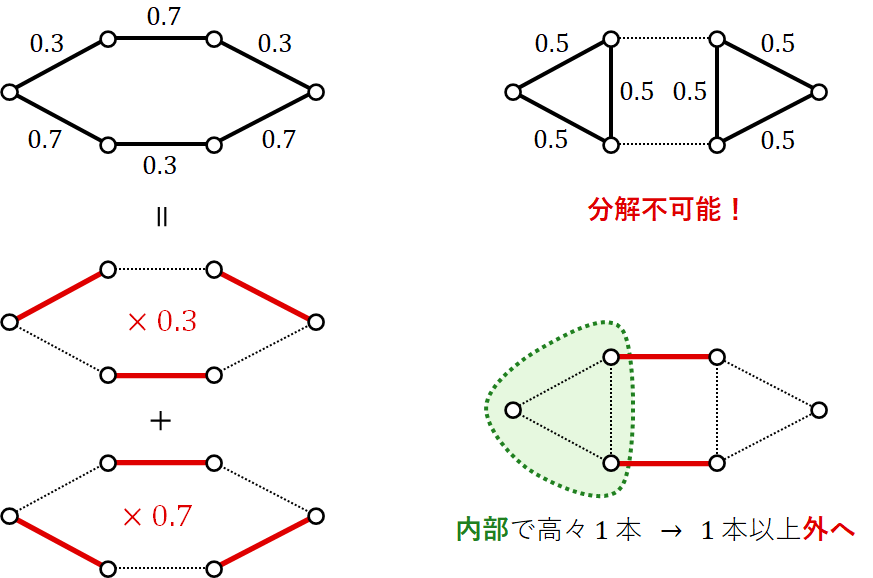



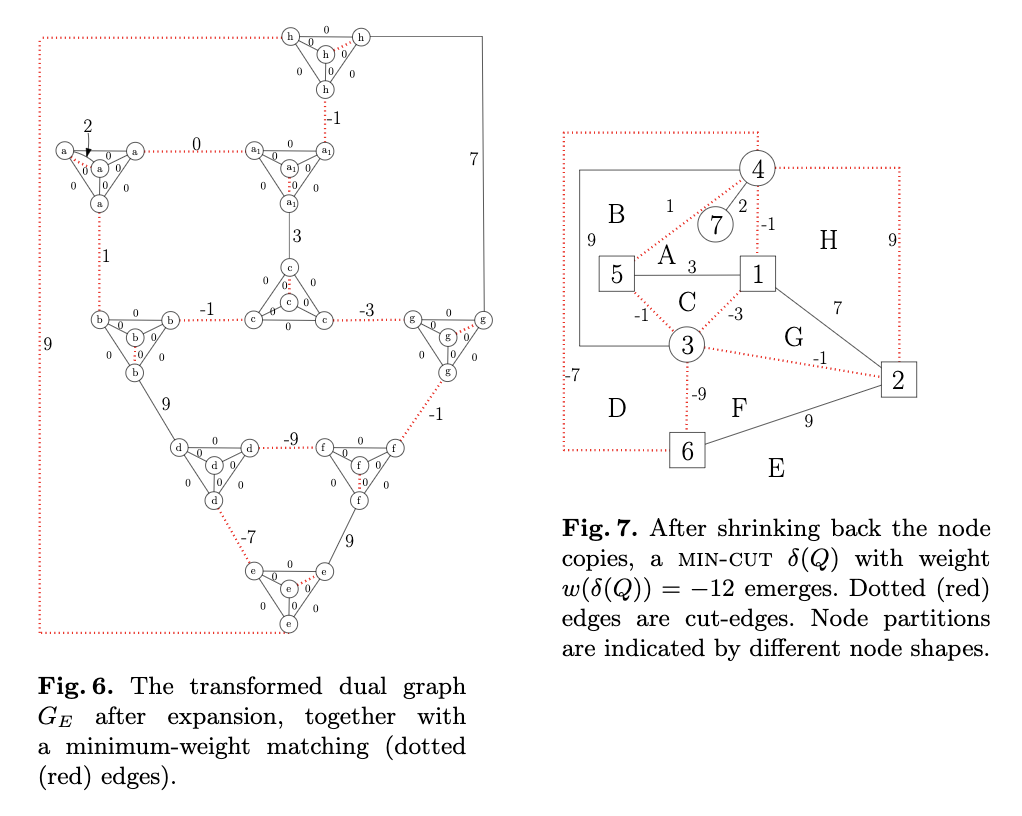
重み付きマッチング概観



グラフ理論
て持ち,双対グラフ上の反応拡散方程式に従う.一方,各信号はループの目標サイクル長に 基づいて自分の周波数を決める.これにより,均一性を維持しつつ,多くの信号にとって好 ましい値へとシステム全体のサイクル長を変化させる. 実環境への適用を考える上で交通流の右折や左折の3 章グラフ理論 (執筆者:高橋俊彦)11 年7 月受領 概要 グラフ理論の起源はEuler によるK¨onigsberg の橋問題(1736 年)といわれるが,数学の 1 分野として認知され始めたのは1900 年代半ばあたりである.Berge は1970 年に自著のま領域分割の双対グラフとは,無向グラフで 各頂点が分割された部分領域に対応し, 各辺が境界を (1 次元的に ) 共有する 2 つの部分領域に対応するもの
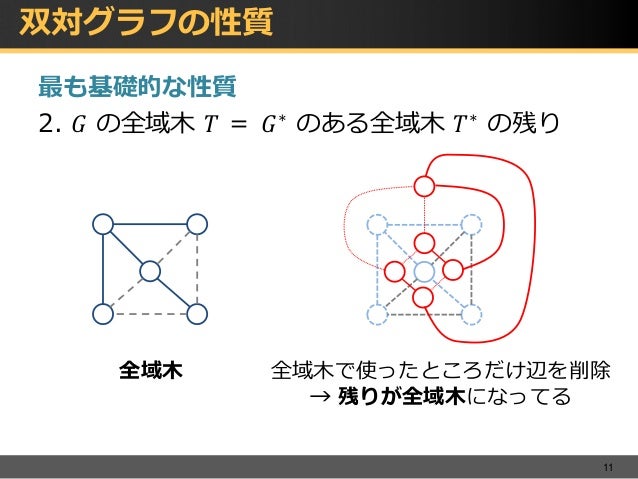



平面グラフと交通ネットワークのアルゴリズム




平面グラフの閉路セパレータ さてもちブログ
線グラフと似ているグラフに双対グラフがあります。 双対グラフとは 平面グラフに対して、「領域を頂点にして、隣接する頂点を辺で結んだグラフ」を双対グラフ( dual graph )といいます。 参考:グラフの双対 平面グラフとは 平面グラフ( plane graph )は、辺が交差しないグラフですグラフ第1軸×第2軸 第1軸と第2軸の最適重みベクトルを用いて作成したラベル付き散布図 参考文献 西里 静彦, "質的データの数量化-双対尺度法とその応用", 朝倉書店, 19 エクセル統計を使えば、Excelのデータをそのまま簡単に統計解析できます。 エクセル統計の購入へ 集計表の作成ずグラフgを対象とした閉路マトロイドm(g) の双対 マトロイドについて考えてみよう 〔閉路マトロイドとカットセットマトロイド〕 グラフgが与えられた時,狐の集合e上で定義され た閉路マトロイドm(g)の双対マトロイド川d(g))*と 33節で定義したカットセットマトロイドm*(g) の聞 には,次の



逆構造定理の略証



グラフ理論の問題を教えてください 2つの同型な平面グラフ 頂 Yahoo 知恵袋
元のグラフにおけるカットセットは双対グラフにおいてタイセットになる 元のグラフにおけるタイセットは双対グラフにおいてカットセットになる ここで, カットセットとは, それらをグラフから取り除くと, グラフが二分されてしまうような枝の集合のことです すなわち, 節点を一般化した第29回コラム 「物事を裏返して眺めてみる-「双対」のススメ」 情報アーキテクチャ専攻助教 森口聡子 双対(そうつい、dual)とは、互いに対になっている2つの対象の間の関係を表す言葉である。 2つの対象がある意味で互いに「裏返し」、「表裏」の双対グラフ(その2) 何本かの枝で囲まれた領域を"点"として, で 表す グラフとネットワーク(第 8回) – p7/18 双対グラフ(その2) 2つの領域が枝aを狭んで隣りあっているとき, これら2つの領域の を破線の枝で結ぶ この 枝をa とする グラフとネットワーク(第 回) – p7/18




Risan Suugaku




双対グラフ Wikipedia
双対グラフで対応する2つの概念を 双対概念(dual concept)という。 たとえば、辺の除去と辺の縮約、ループとブリッジ、偶グラフと2部グラフ、はお互いに双対な概念である。 演習問題 ( → 解答 ) 1. 次数列が ( 7, 6, 5, 4, 4, 4, 1, 1 ) である単純グラフは 双対グラフは特定の埋め込みに依存するので、 平面グラフ の双対グラフは、同じ平面グラフが 同型 でない異なる双対グラフを持つことができるという意味で一意ではない 。 図では、青いグラフは同型だが、その双対の赤いグラフはそうではない。 下の赤いグラフはすべての次数が6未満であるのに対し、上のグラフは次数6の頂点を持つ。 (青いグラフの外側の面に対応する)。と双対グラフの間にどのような関係が成り立つのかを詳しく見て行く 幾何学的双対グラフの作り方 以下の作り方を図に載せたグラフGを参考にしながら見て頂きたい (1) グラフGの各面fの内側の点v∗ を選ぶ ⇒ こうして打たれる点が双対グラフG∗ の点となる (2) グラフGの各辺eに対応させて, e



組合せとグラフの理論 塩田 年度 第10回




平面グラフと交通ネットワークのアルゴリズム
双対, by Wikipedia https//jawikipediaorg/wiki?curid= / CC BY SA 30#数学的構造#双対性#数学に関する記事双対双対(そうつい、, )とは、互いに対になって



問題4



グラフ理論



平面グラフアルゴリズム 競プロ練習記録




9 三色の三角形



グラフ理論



Ieice Org



組合せとグラフの理論 塩田 年度 第10回



グラフとネットワーク 19年度前学期




双対グラフ Wikipedia



組合せとグラフの理論 塩田 年度 第10回




Kbits Pcm 512 Cddat 256 Mpeg 1 128



グラフ理論



組合せとグラフの理論 塩田 年度 第10回



組合せとグラフの理論 塩田 年度 第10回




比較可能グラフは理想グラフ 忘れても大丈夫




Ppt 電気回路学 Powerpoint Presentation Free Download Id




Lp双対性による2部グラフとkonig Egervary定理のマッチング




平面グラフアルゴリズム 競プロ練習記録
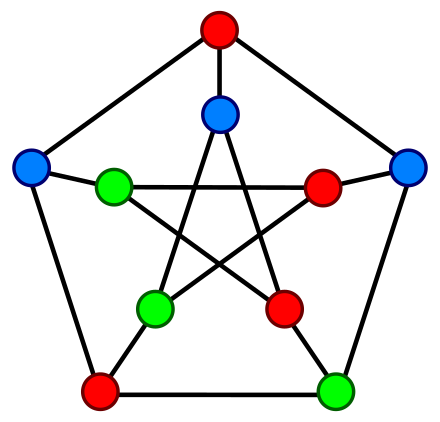



グラフ彩色 Wikiwand



組合せとグラフの理論 塩田 年度 第10回



Ieice Org




Uematsu Y 双対 2種類の点をそれぞれ集めた図なども含めて 視座の移動が感じられてとても面白いです 第294回 グラフ理論 偶奇の伝搬 後編 結城浩 Hyuki 数学ガールの秘密ノート T Co 0pqyxnhqnp
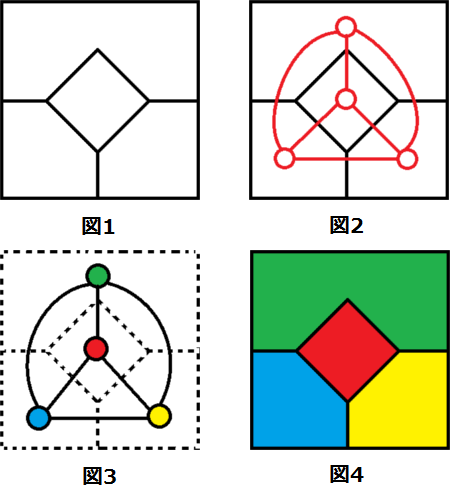



グラフ理論の双対グラフ 平面グラフと平面的グラフ オイラーの定理



Dopal Cs Uec Ac Jp



組合せとグラフの理論 塩田 年度 第10回




双対グラフ Wikipedia




双対グラフ Wikipedia



Theory Of Computing Lab 平面グラフにおける刻み分割構成の分割統治法アプローチ



組合せとグラフの理論 塩田 年度 第10回



Ocw Hokudai Ac Jp




多面体グラフ 多面体グラフの概要 Weblio辞書



Kurims Kyoto U Ac Jp




平面グラフアルゴリズム 競プロ練習記録
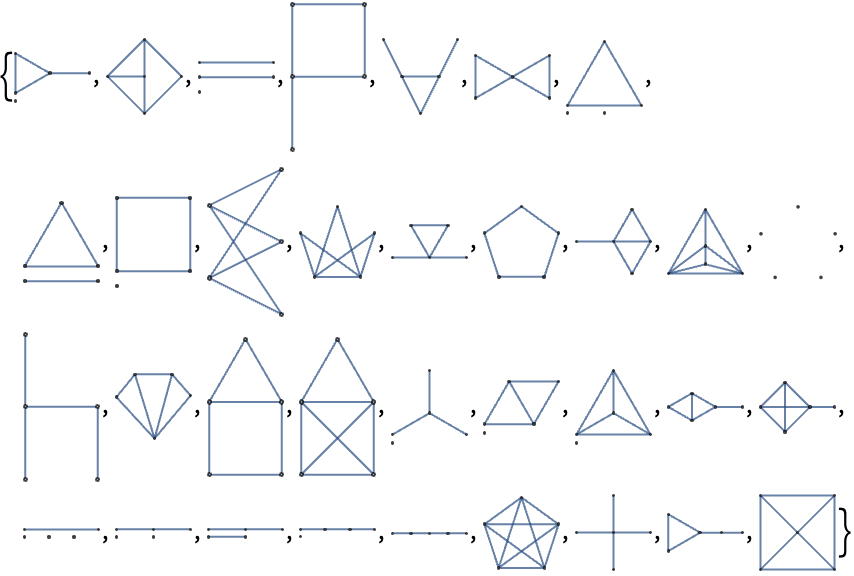



Graphdata Wolfram言語ドキュメント
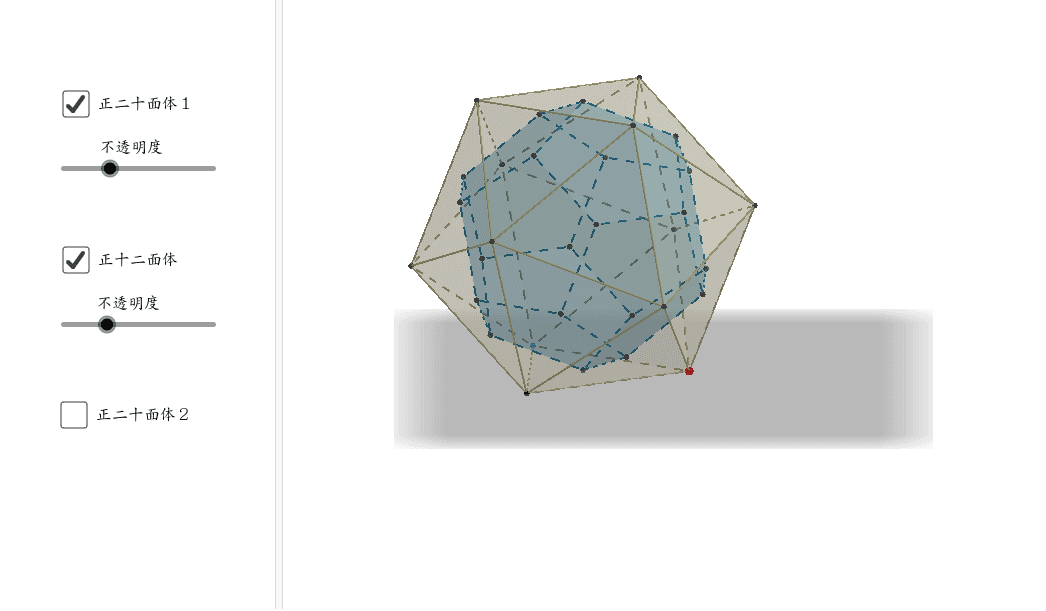



双対多面体 正二十面体 正十二面体 Geogebra




双対グラフ変位3 D レンダリング構成 3dのストックフォトや画像を多数ご用意 Istock




1998 24号 任意オブジェクトのポリゴン描写からパラメトリック表面表現を得るためのシステムと方法 Astamuse
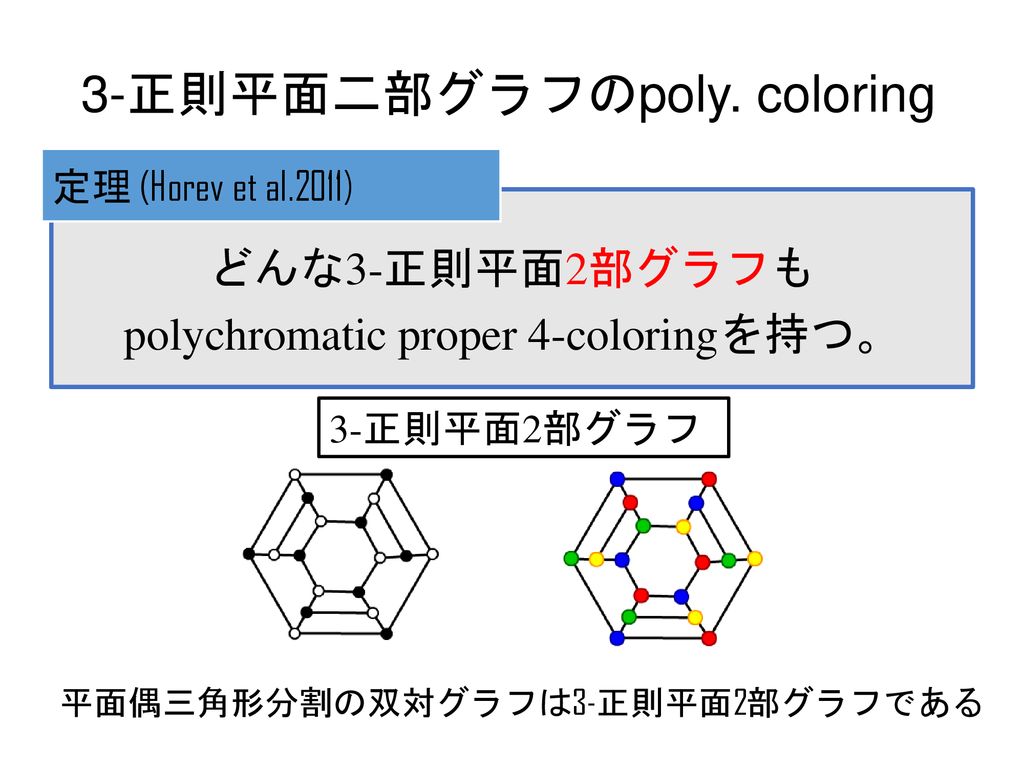



閉曲面上のグラフとグラフ彩色 大阪組合せ論セミナー 共同研究 松本直己 成蹊大学 朝山芳弘 横浜国立大学大学院環境情報学府 Ppt Download
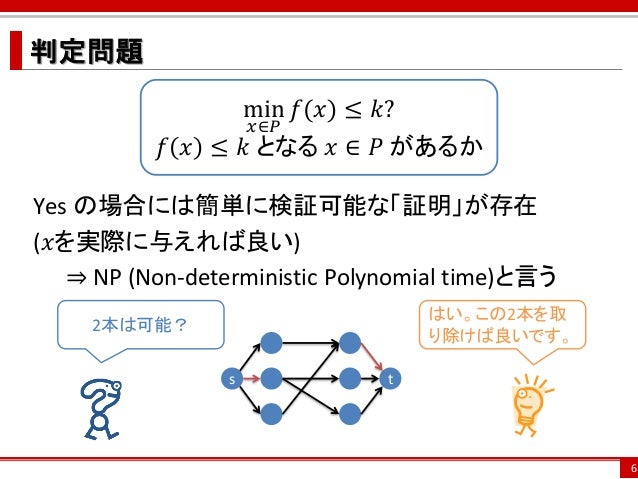



双対性



グラフ理論3
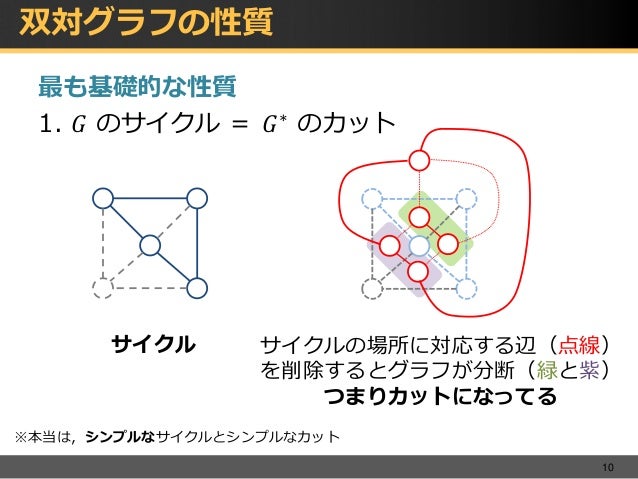



平面グラフと交通ネットワークのアルゴリズム



組合せとグラフの理論 塩田 年度 第10回




双対グラフ Wikipedia




双対グラフ変位ボール 3 D レンダリング 3dのストックフォトや画像を多数ご用意 Istock




最短経路の双対と差分制約 西尾泰和のscrapbox




第299回 グラフ理論 制約が生む世界 前編 数学ガールの秘密ノート 結城浩 Cakes ケイクス



組合せとグラフの理論 塩田 年度 第10回




二部グラフの最小点被覆 最大安定集合 最大独立集合 最小辺被覆を総整理 Qiita




閉曲面上のグラフとグラフ彩色 大阪組合せ論セミナー 共同研究 松本直己 成蹊大学 朝山芳弘 横浜国立大学大学院環境情報学府 Ppt Download




離散数学 双対グラフの書き方について 双対グラフの書き方が分かりません Okwave




平面グラフ



オイラーの多面体定理



Theory Of Computing Lab 有向平面グラフにおけるborradaileとkleinのmaximum St Flowアルゴリズムの実装と検証




双対グラフ Wikipedia



組合せとグラフの理論 塩田 年度 第10回



グラフ理論2



平面グラフと交通ネットワークのアルゴリズム



組合せとグラフの理論 塩田 年度 第10回




双対グラフの意味 用法を知る Astamuse




双対グラフ Wikipedia
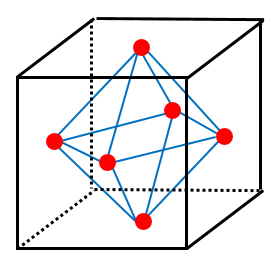



正六面体と正八面体の双対関係と京大の問題 高校数学の美しい物語
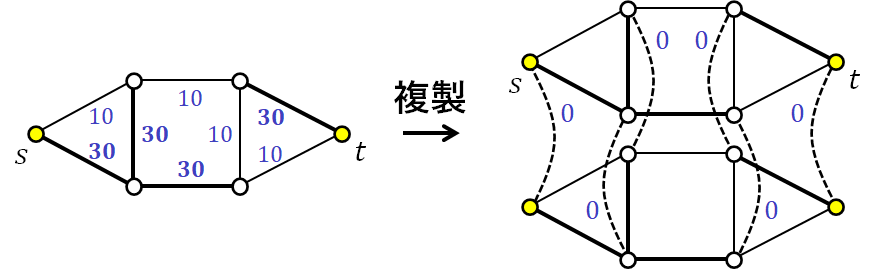



重み付きマッチング概観




Le Algorithm グラフ上での確率過程の双対性



Kurims Kyoto U Ac Jp




ピーターセンの定理 Wikiwand




双対グラフの意味 用法を知る Astamuse




双対グラフ Wikiwand



Ocw Hokudai Ac Jp



双対グラフ カテゴリーの記事一覧 Ryamadaのコンピュータ 数学メモ



双対グラフ




集合被覆問題 3 双対で緩和 決定的に丸める さてもちブログ



グラフとネットワーク 17年度前学期
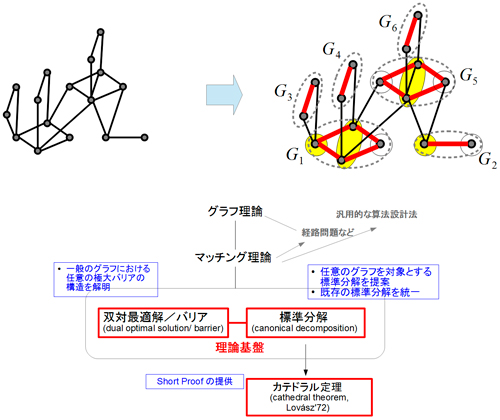



Canonical Decompositions Describing Structures Of Matchings In Graphs 情報処理学会



組合せとグラフの理論 塩田 年度 第10回
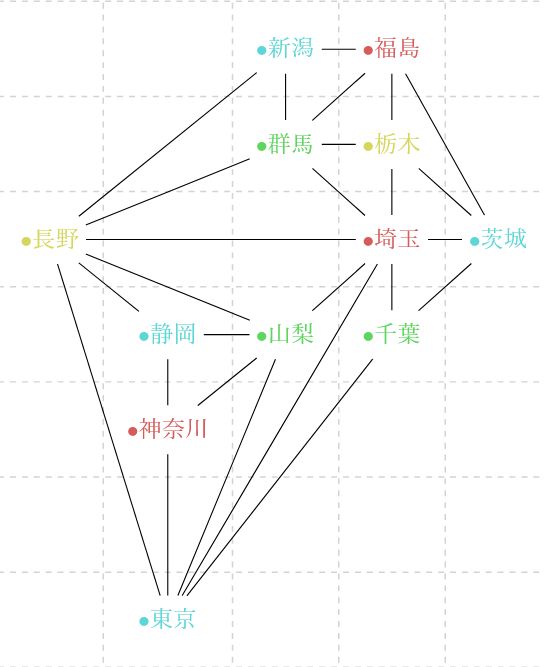



地図の塗り分け グラフの彩色問題 四色定理とは何か 趣味の大学数学



二部グラフの最小点被覆 最大安定集合 最大独立集合 最小辺被覆を総整理 Qiita



双対グラフ Wikipedia



Ieice Org
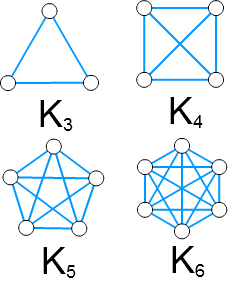



クラトフスキーの定理の証明 1 グラフ理論用語と定理の紹介
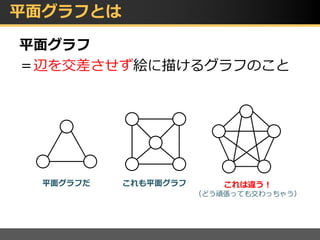



平面グラフと交通ネットワークのアルゴリズム




平面グラフアルゴリズム 競プロ練習記録



組合せとグラフの理論 塩田 年度 第10回




双対 Youtube



Theory Of Computing Lab O Nlogn 最大流アルゴリズムの実装と検証




双対グラフ Wikipedia




1998 24号 任意オブジェクトのポリゴン描写からパラメトリック表面表現を得るためのシステムと方法 Astamuse
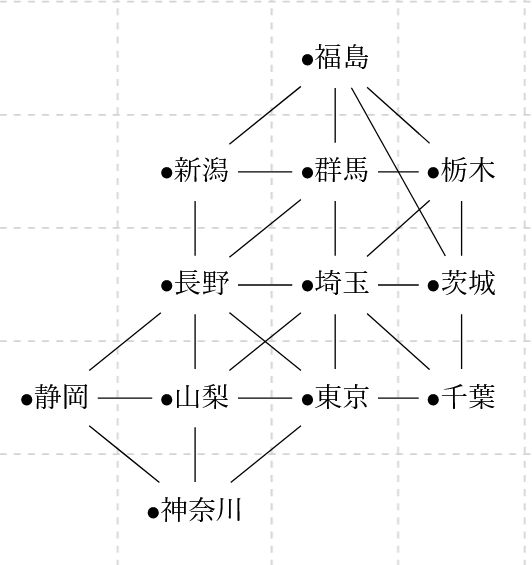



地図の塗り分け グラフの彩色問題 四色定理とは何か 趣味の大学数学




Le Algorithm 木分解は茨の道




モンテカルロ法を用いたボードゲームの対戦プログラム 双対グラフ上の高速プレイアウト手法の提案 計算理論とアルゴリズムの新潮流
コメント
コメントを投稿